音高标识与音律计算

　　音律知识应该是音乐工作者的基本功，无论是作曲者，还是演唱、演奏者，懂得音律，必有利于能力的发挥；而从事音乐研究的人具有一定的音律学知识，可使研究更细致、更深刻；即使是音乐爱好者，具有音律学知识，对于音乐作品的理解深度与欣赏能力的提高，必有明显的帮助。尽管这个道理是人人皆知的，但是多数人对于音律学都不愿意接触，认定音律学乃是一种艰深的学问。这一认识尽管有其其历史根源，却未必正确。

　　律学堪称为我国的国学。自古至今，我国历代律学著作积累颇丰，涉及律学的著作如《管子》、《吕氏春秋》、《淮南子》、“二十五史”……虽然不能说汗牛充栋，却可认定为在世界各国中绝无仅有的。事实上就我国古代的律学著作来说，这些音律学著作也确实存在着不少缺憾：例如将律学的基础研究弄得很琐碎；以“同律度量衡”为口实，硬把律、度、量、衡牵扯在一起；把律与历（法）、天象和候气混搅在一起，从而把律学又弄得很玄。如此等等。所有这些律学研究上存在的问题，都成了人们学习音律学知识的心理障碍。

　　应该承认，“同律度量衡”有其科学的内涵，“度、量、权、衡”是关系人们生活的大事，它得有个统一的标准。如今将黄钟正律管的长度作为“长度”（分、寸、尺、丈）的标准，将黄钟正律管的容积作为“容量”（龠、合、升、斗、斛）的标准，将黄钟正律管内的积实作为“权”（砝码）的标准，从而制定衡器（秤），这确实有其一定的科学性。但是将十二律管的来源神秘化，就未免将问题复杂化。

　　律与历的糅合，乃是因为古代将十二律与十二月令糅合一起的缘故；月令与天象密切相关，因此古代的正史便将“律”与“历”合作一志。

　　除去以上所述人为造成的律学研究神秘因素而外，也毋庸讳言,音律学确实有其艰深的一面。这是因为律学是音乐声学中的一个重要组成部分。人们在解决一些律学理论和乐器制作方面的具体问题时,不少音律学问题涉及到人们至今还难以弄清的音乐声学方面之问题的缘故。笔者认为,律学并不是玄学,在音乐范畴内它是极其重要的应用科学，实用是它的重要属性。因此，有关这方面的音律学知识，还是可以讲得浅显些的。本文打算谈一点这方面的知识。

　　一、音高标识

　　乐曲有一定的调，乐音有一定的音高，我国古代很早就注意到音律和调高了。我国古代音高（绝对音高）是用黄钟、大吕、太蔟、夹钟、姑洗、仲吕、蕤宾、林钟、夷则、南吕、无射、应钟等十二律吕来表示的。黄钟、太蔟、姑洗、蕤宾、夷则、无射等为六律，为阳；大吕、夹钟、仲吕、林钟、南吕、应钟等为六吕，为阴。

　　黄钟（正律），据我国古代典籍记载，乃是径三分、长九寸的闭管律管所奏出的音高；也就是说，管内径为管长的三十分之一，因此，《汉书》就认定管内周为管长的十分之一。由此可知，汉代的圆周率为“周三径一”。康熙帝曾批评这种“约率”，认定用这种约率制作的律管，无论如何都是不会合律的。康熙帝的这一批评近似于诡辩，当然是不正确的。

　　我国古代的律管，无论是铜质的、玉质的还是竹质的，除明代音律学家朱载堉所设计的36支异径律管为开管外，其余都是闭管。朱载堉所设计的律管为开管，这在《律学新说·吹律第八》中有明确的说明。朱载堉说：“尝以新律使人吹之，能吹响者十无一二。往往因其不响辄以指掩下端，识者哂之。”瞧！朱载堉所设计的律管是不能“以指掩其下端”的。这两端通洞的律管不就是开管吗？

　　这种律管不同于一般的箫笛之类管乐器。它有自己特定的吹律方法。这种吹律方法在《律学新说·吹律第八》中也有明确的说明。朱载堉说：吹律时“吹律者须凝神调息，绝诸念虑，新安志定，与道潜符，而后启唇少许，吐微气以吹之，令气悠悠入于管中，则其正声乃发。又要持管端直，不可轩昂上端，空围不可以唇掩之。”

　　这种吹律方法很有其特殊性。律管的末端掩住以后，末端校正量便等于零；吹奏端“空围不可以唇掩之”，则其管端校正量不仅最小，也最稳定，当温度和湿度不变时，律管吹出的频率也就相当稳定。本人曾在上海交通大学的声学实验室内间断地吹过三次测频，所测频率竟完全一致。这也说明，数千年前的古人就具有了相当的声学知识。

　　如今已说清楚朱载堉的异径律管为开管，又何以知道古代的律管惟独朱载堉所设计的律管为开管，而其他律管皆为闭管呢？这就得弄清朱载堉所设计的律管与其他律管直接的差别。原来朱载堉所设计的36支异径律管都开有一个一分七厘六的豁口，而其他律管则没有。别小看这豁口，它有很重要的功用。古人云，“差之毫厘，失之千里”，这小小的豁口就象洞箫的豁口一样，很有利于律管的发声。尽管如此，这开有豁口的律管“能吹响者十无一二”，而没有豁口的律管若不“以指掩其下端”，空围又不以唇掩之，那是根本无法吹响的；而“以指掩其下端”，不但易于吹响，而且发声响亮，音高又十分稳定。这一事实就充分说明古代律管为闭管。所缺憾的是，由于历代度量衡器不同，历代的黄钟正律音高也就大不一致；尽管我国音乐大家杨荫浏先生在《中国音乐史纲》中曾用“律管频率计算公式”计算出了“历代黄钟正律音高”，但是由于“律管频率计算公式”的不严密，所以计算出的频率也就不可信（注一）。

　　如今音高的表示方法，通常都用A、B、C、D、E、F、G七个英文字母及升降符号来表示十二律之音高。这种音高的表示方法，由于用途的不同而有所差异。具体地说，就是有物理学和音乐学两种不同学科的两种不同音高表示方法。物理学上的音高表示方法，用的一律为大字元号，即:C0、#C0、D0、bE0、E0、F0、#F0、G0、bA0、A0、bB0、B0；C1、D1、E1、F1、G1、A1、B1；C2、D2、E2、F2、G2、A2 、B2；……。音乐上音高的表示方法与物理不同，它有大字组和小字组两类，大小字组又以阿拉伯数位表示组别。例如大字二组：C2、#C2、D2、bE2、E2、F2、#F2、G2、bA2、A2、bB2、B2；大字一组：C1®B1；大字组：C®B；小字组：c®b；小字一组：c1®b1；小字二组：c2®b2；……。

　　关于标准音有两方面的内容，一是物理音高，一为音乐音高。物理音高的中央C为256Hz（赫兹），其优点是256可以被2整除，C0为16Hz。音乐上的标准音分第一国际音高和第二国际音高。第一国际音高是1834年物理学家在德国司徒嘉特会意上决定的为a1=440Hz；第二国际音高是1859年在法国巴黎召开的音乐与物理学家会议上决定的，a1=435Hz。如今由于工业的发达，国际音高有升高的趋势。

　　这儿需要说明的是，音乐上的c1就是我们通常所说的中央C，它相当于物理音高的C4。

　　音乐上的C2音，相当于物理音高C0。所谓的国际音高，音乐上音高的表示方法为a1，而物理学上则用A4。音乐和物理的两种音高表示方法，其在音名的表示方法上，有两组容易混淆，即音乐上的大字一、二组和物理上的大字一、二组，其余各组则不可能混淆。至于音乐上的C2（大字二组，相当于物理上的C0），其频率为16.35Hz。

　　物理学为什么把16Hz作为C0呢？原来16Hz是人耳所能听到的最低音，低于这个频率的声波被称作“次声”。次声乃是人耳无法听见的声音。

　　在音乐研究或音乐考古工作中,我们常常需要对一些乐器的音高进行检测。这些乐器上所发之音,当然不可能同今日所规定的标准音一致,往往不是比某音高,就是比某音低。为了能体现出某音的准确高度，通常都借助音分来表示。例如E4+38，或者F5-45等。我们不难看出，这E4+38所用的乃是用的物理学上的音高表示方法。由于物理学上的E4，就是音乐学上的e1，故而物理学上的音高E4+38就是音乐学上的e1+38，也就是说，该音比e1音要高38音分。又如F5-45音分，由于物理学上的F5，就是音乐学上的f2，故而F5-45就是比f2低45音分的音。

　　E+38及F5-45的音高表示法，又可以用音分来表示:E4+38可以写成5238音分，F5-45可以写成6455音分。这又是什么道理呢？原来十二平均律的一个八度是1200音分，C0乃是0音分，C1便是1200音分，Ｃ4便是4800音分，E4是5200音分，E4+38当然就是5238音分了。

　　音高还有另一种表示方法，那就是用频率来表示。例如E4+38的频率是336.94Hz，F5-45的频率是680.54Hz。这种种计算方法，下文将作专门介绍。

　　这儿还要指出一点,那就是尽管频率不变,若标准音有所变动,音程也就会随着变动。例如第一国际音高a1的频率为440Hz，第二国际音高a1的频率为435Hz；这两个音相差已达19.79音分。再就c1来说，a1若为440Hz，c1的频率就是261.63Hz；a1若为435Hz,那么c1的频率就是258.65Hz。

　　二、律制种种

　　无论是演唱还是演奏,只要涉及音准就必然要涉及到律制,不同的律制有不同的音准标准。如今世人公认的三大律制，根据其出现的先后分别为三分损益律、纯律和十二平均律。当然,除了这三大律制而外,还有不少不十分规范的“律制”。笔者认为,这些所谓不十分规范的律制，乃是由于它们不像三大律制那样有明确的生律方法，而仅仅是靠着对演奏的测频所下的结论，例如不少专家对我国民间所用的均孔笛演奏实际所定义的“七平均律”，以及除十二平均律以外的众多“平均律”。由于本文乃是介绍音律计算的，旨意不在讨论律制，故而只介绍三大律制，对所谓的“七平均律”，以及其他众多的“平均律”不作讨论。

　　（一）三分损益律

　　三分损益律乃是用三分损益法生成。此律亦被称作五度相生律。五度相生律，据说乃是希腊哲学家毕达哥拉斯所发明。三分损益法是用振动物体分成三份，损其一份以生成上方五度音，益其一份则生成下方四度音。由于三分损益律所用振动实体之比例为4:3及2:3，故而现代音律学家吴南熏称它为“简律”。

　　我国最早记载三分损益律的著作是《管子》。管子（仲）与毕达哥拉斯生活的年代差不多。尽管有不少专家在研究五度相生律与三分损益律的异同，但是笔者认为，五度相生律和三分损益律的本质乃是相同的。不过五度相生律所生各律不在一均（一个八度）之内，就以c1来说，用五度相生法生成的第12律乃是f7而不是f1，因此得移低6组（即除以64）；若此，它的生律方法不仅与三分损益律完全相同，而又远不及三分损益律明了。

律名	黄钟	大吕	太蔟	夹钟	姑洗	仲吕	蕤宾	林钟	夷则	南吕	无射	应钟
音程	0	113.69	90.22	113.69	90.22	113.69	90.22	90.22	113.69	90.22	113.69	90.22
音名	宫		商		角		变征	征		羽		变宫
音程	0		203.91		203.91		203.91	90.22		203.91		203.91

　　三分损益律十二律的生律顺序依次为：黄钟®林钟®太蔟®南吕®姑洗®应钟®蕤宾®大吕®夷则®夹钟®无射®仲吕。这十二律吕由黄钟始，阳律生阴吕，阴吕又生阳律。现将十二律相邻二律之间的音程（音分）,以及黄钟宫七声之间的音程（音分）列表于下（单位：音分）：

　　三分损益律的各个半音之间的音程是不等的，有大半音与小半音之分。因此从黄钟生律十二次以后就无法回到黄钟，而只能是比黄钟高一古代音差的黄钟变律。由于古人曾把律与历糅合在一起，西汉末年的音律学家京房就将三分损益律演算到第六十律，南北朝时的钱乐之更是演算至第三百六十律，以求“一日当一律”。

　　三分损益律就十二律来说，无论是“损一”还是“益一”，就是算齐十二律备查，也并不十分繁难；但是要算全三百六十律就不轻松了。过去曾有人算全三百六十律，再加上细心的验算，耗时达数月之久。本人就无意这浩繁的“工程”，因此归结出了“三分损益律”算式。该算式为logfn=logf0[nlog3-（n+a）log2]，其中的a为n乘以[（log3-log2）/log2]的整数部分。

　　（二）纯律

　　纯律的出现晚于三分损益律。它的大二度、四度、五度与三分损益律无异；而大、小三度却与三分损益律有明显的差别。由于大三度为386.31音分，小三度为315.64音分，故而完全应该认定,这音调同泛音相关。因为三分损益律中的纯五度乃是3:2（三分损一），纯四度乃是4:3（三分益一）。若从泛音列的角度考虑，弦的1/3与1/2处的泛音之间的音程正好是纯五度，弦的1/4与1/3处的泛音之间的音程也正好是纯四度。现在再来看看纯律的大三度，正好是弦的1/5与1/4处泛音之间的音程；纯律小三度乃是弦的1/6与1/5处泛音之间的音程。为此，纯律各相邻二音之间的音程为：

音名	宫	商	角	清角	征	羽	变宫
音程	0	203.91	182.4	111.73	203.91	182.4	203.91

　　从以上所列三分损益律和纯律的音程来看，其音程最明确的特征便是各音之间的音程不等。从理论上分析,音程不等必然给旋宫转调带来不可逾越的障碍。千百年来,人们一直在寻求解决的办法,最后终于寻到了十二平均律。

　　（三）十二平均律

　　十二平均律与三分损益律、纯律等自然律制不同，他是人工律制，即人为创造的律制。发明十二平均律的是明朝郑王世子朱载堉（1536——1611）。

　　十二平均律又称十二等律，即一组（我国古代称一均）十二个半音，每相邻的半音比值相等。十二平均律的生律公式为2-1/12，相邻二律之间的频率比为1.05946309436,相邻二律之间的弦长比为其倒数：0.943874312681。无可讳言，十二平均律虽然解决了旋宫转调的难题，但是这一人工律制同纯律音程相去甚远，所奏的和弦必然远不及纯律协和。正因为这个缘故，所以有经验的钢琴调音师在为钢琴调音时，就自然而然地给钢琴各音之间的音程关系作一点微小的技术处理。

　　钢琴所用既然为十二平均律，那么从理论上说，各音（律）之间的音程应该是相等的。我们无法依据调音师的经验来作音律分析。因此，从理论上来说，十二平均律的各律（半音）之间的音程就理当认作100音分。

　　除这三大律制而外，还有一些别种律制。在我国讨论最热门的要算所谓的“七平均律”了。这种律制的历史已够悠久了。据笔者考证，它被我国民间音乐（所谓的“俗乐”）所采用，至迟是在魏晋时期，因此至少有1800年以上的历史了。尽管这种应用已很久的律制为民间俗乐律制，但是魏晋时期就已用于宫廷“雅乐”之中，这也是历史的事实。这一史实不仅有日本现存的法隆寺所藏隋朝的“笛”、八支分别用象牙、玉石和竹制作的唐朝尺八为证，更有《晋书》和《宋书》的记载为证。笔者通过对《晋书》所载“荀勖笛律”的多年研究，以及对“荀勖笛律”所涉及的“泰始笛”的制作研究，同样证明《晋书》和《宋书》的记载可靠。

　　（四）“七平均律”

　　这儿讨论的所谓“七平均律”，杨荫浏先生曾经称其为“等差律”。后来杨先生又认为这“等差律”的名称未必恰当，因它是弦或管等振动实体的近于均等，故而主张该律应正名为平均律（注二）。不过杨荫浏先生所说的平均律同今日人们所说的“平均律”乃是名同而实异的两个概念：杨荫浏先生所说的平等律乃是振动实体的均分，却不是他一贯反对的八度音程的均分。

　　关于“七平均律”一名的由来，尚缺具体的资料。这一名称的出现至迟在民国三十六年。这有杨荫浏、查阜西二位先生的论争文章为证。而提及“七平均律”的“理论”，乃是清末的戴武。郑颖荪先生曾收藏戴武于光绪年间写的《律说》一书，戴武于该书中明确地提出了“七平均律理论”。大家都知道，清朝自康熙帝始，就对朱载堉的平均律及异径管律进行了批判。戴武也提出了朱载堉不该用“十三律连比例开十一乘方法”，而应该“用八律连比例开六乘方法”。在戴武看来，一均（一个八度）分成十二个半音，相邻二音之间为100音分是不对的；应该分成八个音，相邻二音之间的音程应该是171.43音分。

　　杨荫浏先生一直认定这一“理论”是背离中国音乐之实际的。笔者40多年前就利用课余时间向民间艺人学笛，40年前亦常听吾师甘涛教授之尊人甘贡三老太爷奏笛，当时还开始了箫笛的制作。对于箫笛的研究不敢说有成，但至少不是“不甚了了”。如今不论是从这旧式均孔箫笛“一笛七调”的演奏情况，还是从汉魏以来的笛子制作工艺的要求来看，这所谓的“七平均律”，都是同旧式均孔笛相关的。要把这问题说清楚，就必须弄清管口校正的问题。由于管口校正研究具有相当的复杂性，故而如今尚无法从音律学以及音乐声学的角度进行阐述。如今人们所引用有关“七平均律”的资料，都是对演奏音响的实测，资料都是因人而异、因时而异，难作准则，笔者认为无从讨论。

　　演唱或演奏过程中，音准是以律制为标准的。但是演唱或演奏中的音准又具有相当的灵活性，即演唱或演奏的音准必然存在一定的误差，与以律制为依据而整齐划一的演唱或演奏是不存在的，若不允许演唱或演奏过程中存在误差，我们必将失去丰富多彩的音乐生活。

　　三、音律计算

　　本文讨论音律的计算方法之目的，乃是为着能有利于音律学论文的阅读，有利于演奏、演唱技能的发挥。尤其是从事音乐研究而又不擅长音律计算的人，若能掌握音律计算方法，于研究无疑是大有俾益的。本文将讨论音分与频率的转换、音程与频率的转换、弦上音位的计算等等。至于管乐器上的音位计算，由于管子上的“管口校正”情形的复杂性至今未能摸清，也就无法叙述，无从讨论。当然，本人的研究所得出的结论是，影响管乐器频率不光是管口校正，更有声波速度的影响。这是本人四十多年箫笛制作研究所得出的结论，有待于声学实验的验证。

　　（一）绝对音高与频率的换算

　　绝对音高有两种表示方法，一种是音分表示法，另一种是音名表示法。在考古研究中，已如前文所述，音名是不用音乐上通用的大字组、小字组之区别的，而是仅用大字的0、1、2、3……来表示。起始音是C0，它乃是0音分，一组为1200音分。例如，A4便是5700音分。这是因为C0——C4为4800音分，C4——A4为900音分，二者之和也就是5700音分了。再如bB5-34便是6966音分。这是因为C0——C5的音程为6000音分，而C5——bB5为1000音分，计7000音分，减去34音分，也就是6966音分了。

　　附带说一句，若将考古上的音高换算成音乐上的音名表示法也是不难的。这儿只要记住两个关键性的音就行了。一个是考古学上的C0就是音乐上的C2（大字二组），另一个是考古学上的C4，就是音乐上的c1（小字一组），因此，考古学上的A4，就是音乐上的a1（小字一组）。此外，6966音分就是bb2 -34。

　　关于音分及音名同频率的换算就比较麻烦了。例如6966音分，或bB5-34，它的频率该是多少Hz（赫兹）？要进行计算，首先要记住两个资料：一个是考古学上的C0，也就是音乐学上的C2（大字二组）的频率16.3515978313Hz，取约值16.35Hz；此频率的对数便是1.21356019708。另一个资料便是比例常数3986.31371386，此资料乃是1200/lg2。因为一个八度为1200音分，其频率比为2的缘故。如果我们要求出6966音分的频率，可通过以下计算求得：

　　6966¸3986.314+1.21356 = 2.961，然后查反对数，得914.20（Hz）。这914.20Hz就是6966音分的频率。

　　相反，若知道频率，完全可以运用上述公式的逆运算求得它的音分。例如，已测得考古发掘出的某磬片的频率为586.86Hz，求此音的音分及音名。

　　解：(1) 先求出586.86Hz的对数与16.35Hz的对数之差。

　　lg586.86——lg16.35 = 2.7685345029——1.213560197 = 1.554974312‚ 将1.55497431253986.31371386 = 6196.62。取出近似值6197音分。

　　由于C4为6000音分，D4为6200音分，故而6197音分为D4-3。

　　（二）弦上的音位计算

　　在弦上进行音位计算，其主要目的虽然是为着律学的研究，但是它同样有着实际的用途。最早将弦用于律学计算的是西汉末年的京房（前77——前37）。他为了研究60律而设计了弦准。对于律学研究来说，若要区别三分损益律、纯律、十二平均律三种律制之间的差别，除了借助弦而外，是没有任何一种乐器是能负起此任的。诸君若于此有兴趣，笔者于下方列出这三种律制各音在弦上的百分比。

　　在列出这三种律制音阶各音在弦上的百分比之前，有4点说明。

　　1、三分损益律的传统七声音阶，只有变征（#4）而不用清角（4），纯律只有清角而没有变征。为了统一起见，此处根据如今的音乐实际，也改用清角。

　　2、纯律，实际上乃是在三分损益律的基础上增添了4:3的纯四度、5:4的纯律大三度和6:5的纯律小三度。笔者至今也未曾见到有人介绍纯律的十二律。因此，本文也只能介绍这三种律制的七声音阶在弦上的百分比。

　　3、三分损益律的首律是黄钟，如今人们通常以C（c1）为首音，更有不少人爱把黄钟正律说成C。实际上我们无法证明古代的黄钟就是C，但却可以把黄钟比拟作C。

　　4、在同一根弦上进行三种律制的音程比较时，弦的下端为起点0，上端为止点，即全弦长1。

　　现将三种律制各音在弦上的比例列表于下：

阶名	1	2	3	4	5	6	7	1
三分 损益	1	0.8888	0.7901	0.74	0.6667	0.5926	0.5267	0.5
纯律	1	0.8888	0.8	0.75	0.6667	0.6	0.5333	0.5
十二平均律	1	0.8909	0.7937	0.7492	0.6674	0.5946	0.5297	0.5

　　至于弦上的音分计算当然并不仅仅是为着三种律制的比较。本世纪四十年代，我国音乐大家杨荫浏先生在进行音律研究时，就是借助了弦准，即在弦上确定一标准音，然后确定所测之音在弦上的按弦点，通过按弦点同弦上的基准点的比例，算出所测之音的音高或音程。例如一根长58公分的弦，音高（空弦音）为d1（293.66Hz），现测得某音与弦上47.65公分处所发之音等高，算出所测之音的高度（频率）。

　　解：由于频率同弦长成反比，所以所测之音同空弦音的音程，即为这两段弦长的对数差与音分计算比例常数之积。列式如下：

　　（lg58——lg47.65）´ 3986.314 = 0.08537 ´ 3986.314 = 340.31（音分）。

　　由于d1比c1高大二度，故而d1为5000音分，今再加340.31音分，故而为5340.31音分，其音高为F4+40。运用前面述及的音分同频率换算的方法，可列出以下算式：

　　5340.31¸ 3986.314 + 1.2136 = 2.5533

　　查2.5533的反对数为357.52，由此可知，该音的音高为357.52（Hz）。

　　关于弦上的频率及音位计算，只能计算其相对音高，不能计算其绝对音高。弦的绝对音高的确定必须凭藉其他能确定绝对音高的乐器。正因为这个缘故，汉代的京房既明确指出“竹声不可以度调”，而在涉及弦准的绝对音高时又不得不牵涉到律管，晋代的杨泉也认定“以管定音，以弦定律”。

 

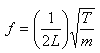
　　何不能确定绝对音高呢？这从弦的频率公式的分析中就可以获得证明。弦的频率公式是：

　　从弦的频率公式可知：虽然弦的频率（F）与弦长（L）成反比，同弦的张力（T）的平方根成正比，同弦的质量（m）的平方根成正比。作为弦乐器上的弦，尽管弦成可以测量，但是其张力与质量都是无法准确测定的，因此频率（F）也就无法确定。

　　（三）从频率计算音分

　　从频率计算音分是比较简单的。它与弦上的音位计算正好为逆运算。若两个频率分别为1362.76Hz与1485.95Hz，求这两个频率之间的音程。可列出以下算式：

　　（lg1485.95lg——1362.76）´ 3986.314 = （3.172 ——3.134）´ 3986.314

　　= 0.038´3986.314=151.48（音分）。

　　（四）关于板乐器及管乐器的频率

　　音律既然是乐器的重要属性，那么除了弦乐器而外，还有打击乐器和管乐器。打击乐器如钟磬，属于板振动。板振动的固有频率的计算，乃是凭藉的经验公式，因此除了可以对它测出的频率进行计算而外，目前还无法对它本身的固有频率进行计算。

　　作为板振动的钟磬，尤其是特殊的板振动的乐器——钟，据说西周就有所谓“立均出度”的“均钟木”。尽管东周出土的钟磬有校音的痕迹，但是所校音高的范围不大。由此可见，自西周始，用这“均钟木”来铸造具有绝对音高的钟磬是完全可信的。但是这“均钟木”究竟是如何“立均出度”的，如今已成了难解之谜。

　　至于管乐器，常常见到人们述及它们的频率公式或音程公式，看起来管乐器的固有频率似乎是完全可以计算的。实际上管乐器除了可以对它们所奏出的音高进行计算而外，作为乐器的固有频率（频率公式）或音程公式，目前还无法进行计算。以下略述其原因。

　　首先就管乐器的基频公式来说，其频率应该同声波速度成正比，同气柱的长度成反比。这看上去似乎很简单，但是其真实情况却不是这么简单。原来管乐器不仅有开管乐器和闭管乐器，笔者还发现另有开管与闭管的结合型的管乐器。就开管与闭管来说，以边棱音为激振源的笛类乐器，与簧哨乐器的情形又明显不同。例如笛类乐器中的箫笛，其两端与外界大气相接，因此两端都有管口校正量，作为闭管的我国古代律管和排箫，只有一端与外界大气相接，因此只有一个管口校正量。而就簧哨乐器来说，尽管其吹奏端已含于口中或与唇紧密相接，却仍然有开管与闭管之分。例如中国的筚篥、管子与巴乌，外国的单簧管等都是闭管，中国的唢吶，外国的双簧管、大管、萨克斯管，以及各种号，都是开管。那么簧哨乐器中的开管乐器应该有一个还是两个管口校正量？这恐怕是我们的物理学家们还没有认真考虑过的问题吧？

　　再就最简单的笛类乐器来说，律管和排箫的情形应该是一样的，二者之间的管端校正量（因为是闭管，应该只有一个管端校正量）是否应该相同？再就箫笛来说，其声学情形更是完全相同的。可是所有制作箫笛的人都知道，确定笛子音孔位置的公式绝对不适宜于确定洞箫的音孔位置。这是什么道理？原来箫和笛的音调不同而导致管长不同，即使管口校正量相同，其音孔位置的比例也必然不同；实际上箫和笛的管口校正量也确实不同，所以确定音孔位置的方法也就必然不同。

　　欲求管乐器的计算频率（不是实测），必须求得频率计算公式；欲求管乐器的频率计算公式，必须求得管乐器的管口校正量和管乐器中振动着的气柱的声波速度。可是别说各种管乐器的管口校正量各不相同，就是管乐器中的声波速度如今也多是借用了大气中的速度，这显然是未必切合实际的。

　　基于以上分析，可知有关音律计算方面的问题，无论是弦律还是管律，都有许多有待深入研究的内问题。我们在这方面所知的确实还太少。

　　注释：

　　注1.请参阅拙文《黄钟正律析——兼议律管频率公式的物理量》，载南京艺术学院学报《艺苑》（音乐版）1989年第1期。

　　注2.见杨荫浏先生为1950年上海万叶书店出版缪天瑞先生所着《律学》一书的序言。